Defects of vision and correction

 

WHAT HAPPENS WHEN CILIARY MUSCLES CANNOT ACCOMMODATE EYE LENS?

 

This happens when ciliary muscles become weak and cannot adjust the focal length of the eye lens. This may be due to ageing or some other reasons of lack of vitamins, etc

When proper accommodation of eye lens is not done then it leads to defects of eye. We have mainly three defects of vision. They are:

 

1)    MYOPIA (SHORT SIGHTEDNESS): this defect is due to failure of adjusting maximum focal length of eye lens to 2.5 cm when seeing the far objects.

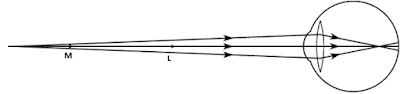
The people with this defect have far point (M). And beyond far point the objects are not seen because f_max for these people will be less than 2.5 cm. So image forms in front of retina. So these people can see a blur image of far objects (beyond M). So these people can see the objects only between least distance of distinct vision (L) and far point (M).

 

Far point: the extreme point from where an object appears clearly to a person with myopia is called far point.

 

Observe the below ray diagrams which represents the defect of myopia:

In the above figure we can see that object is at infinity and a parallel beam of rays from the object enters eye and forms image before retina.

 

In the above figure we can see that object is beyond far point (M). So image is formed in front of retina.

In the above figure it is clear that when object is exactly at far point then image is formed on retina.

From the above figure it is clear that when the object is between far point and least distance of distinct vision then sharp image is formed on retina.

 

CORRECTION:

The eye lens can form clear image on the retina, when an object is placed between far point and point of least distance of distinct vision. If we are able to bring the image of the object kept beyond far point , between the far point and the point of least distance of distinct vision using a lens, this image acts as an object for the eye lens. This can be made possible only when a concave lens is used (recall image formation by refraction through a concave lens).

How can you decide the focal length of the lens to be used to correct

myopia?

 

To correct one’s Myopia, we need to select a lens which forms an

image at the far point for an object at infinity. We need to select bi-concave lens to achieve this. This image acts like an object for the eye lens. Hence the final image is formed on the retina. Let us find the focal length of this bi-concave lens.

Here object distance (u) is infinity and image distance (v) is equal to distance of far point.

u = - ∞ ; v = distance of far point = -D

let ‘f’ be the focal length of bi-concave lens.

Using lens formula, 1/f = 1/v – 1/u

1/f = 1/ -D 􀁂 f = -D

Here ‘f’ is negative showing that it is a concave lens.

HYPERMETROPIA (FAR SIGHTEDNESS):

People with this defect cannot see near objects. These people have near point. They can see the objects behind the near point (H).

The point of minimum distance at which the eye lens can form an image on the retina is called near point (H).

 

Hypermetropia cannot see objects placed between near point (H) and point

of least distance of distinct vision (L).

Image is formed back of retina (appears blur) when the object is between near point and least distance of distinct vision.

  A sharp image is formed on retina when object is exactly at near point

A sharp image is formed on retina when object is behind near point

CORRECTION:

To correct the defect of hypermetropia, we need to use a lens which forms an image of an object beyond near point, when the object is between near point (H) and least distance of distinct vision (L). This is possible only when a double convex lens is used.

 To find the focal length of lens, let us consider that the object is at point of least distance of distinct vision (L). Then the defect of vision, Hypermetropia, is corrected when the image of the object at L is formed at the near point (H) by using a bi-convex lens as shown in figure. This image acts like an object for the eye lens. Hence final image due to eye is formed at retina

Here object distance (u) = -25 cm (least distance of distinct vision)

Image distance (v) = distance of near point = -d

Let ‘f’ be the focal length of bi-convex lens.

Using lens formula, 1/f = 1/v – 1/u

1/f = 1/ -d – 1/(-25)

1/ f = -1/d +1/25

1/ f = (d – 25)/25d

f= 25d / (d – 25) (f is measured in centimetres)

We know that if d > 25cm, then ‘f’ becomes +ve  i.e., we need to use biconvex lens to correct defect of  hypermetropia.

Presbyopia

 

Presbyopia is vision defect when the ability of accommodation of the eye usually decreases with ageing. For most people the near point gradually recedes away. They find it difficult to see nearby objects clearly and distinctly.

 This happens due to gradual weakening of ciliary muscles and diminishing flexibility of the eye lens. This effect can be seen in aged people. Sometimes a person may suffer from both myopia and hypermetropia with ageing . To correct this type of defect of vision we need bi-focal lenses which are formed using both concave and convex lenses. 

Its upper portion consists of the concave lens and lower portion consists of the convex lens.

It is represented symbolically as

 

The upper portion is concave and the lower portion is convex.

Usually doctors, after testing for defects of vision, prescribe corrective lenses indicating their power which determines the type of lens to be used and its focal length.

 

Power of lens:

 

The degree of convergence or divergence of light rays that can be achieved by a lens is expressed in terms of its power.

The reciprocal of focal length is called power of lens.

Let ‘f’ be the focal length of lens.

Power of lens P = 1 / f (in m); P = 100 / f (in cm)

The unit of power is dioptre.

It is denoted by the letter ‘D’.

Example1

Doctor advised to use 2D lens. What is its focal length?

Solution: Given that power of lens P = 2D

Using, P = 100 / f (in cm); 2 = 100 / f

Therefore, f = 100/2 = 50 cm.

The lens has focal length, f = 50 cm.

                thank you